Problem Statement: Determine the physical (real-world) co-ordinates of an object in a scene using a single camera. Concretely, if a reference object (a red cube) is within the field-of-view of oroboto’s camera, determine its position such that oroboto can drive to it. Recall that by dead reckoning, oroboto is aware (more or less) of its own physical co-ordinates within a two-dimensional local frame of reference.
Terminology
In this post the term physical co-ordinates refers to the (x,y) co-ordinates of something in oroboto’s local co-ordinate system / frame of reference. These co-ordinates are specified in units of centimeters and are relative to the location that oroboto was initially powered on, which is considered (0,0) in the physical co-ordinate system.
The term pixel co-ordinates refers to the (x,y) co-ordinates of a given pixel within an image.
Introduction
If we can isolate a reference object within an image we still only possess its pixel co-ordinates: we need a way to convert those to the physical co-ordinates used by the robot.
In this post I’ll discuss using OpenCV to isolate a reference object and then a technique to estimate its physical co-ordinates using only the image from a single camera. A common computer vision (CV) method of determining distance to an object from a camera lens is to use two cameras and the principle of stereoscopic vision to measure depth. While it’s possible to connect multiple cameras to a single Raspberry Pi I wanted to avoid the extra current draw and bulk. I also thought it would be interesting to see the accuracy I could achieve using a simpler approach.
Reference Object, Prerequisites and Assumptions
This technique estimates the physical co-ordinates (x,y) of a reference object (a red cube) of known physical width and height within oroboto’s local frame of reference.
A prerequisite to using the technique is to measure the relationship between the physical dimensions of the cube and how big it appears, in terms of pixels, at various distances from the camera lens. To do this I simply placed the camera at a fixed position and set down a line of markers on the floor at 10cm intervals.
![]()
I then took successive images of the cube at each marker and measured how many pixels wide it appeared at each distance. With a table of physical distance (10cm, 20cm, … n cm) and pixel mappings I calculated a regression to get the line of best fit in Excel at arrived at the following pixel-to-distance equation:
![]()
If we’re able to isolate the reference object in an image and measure its width in pixels this formula can be used to estimate how far it physically is from the camera lens. This technique makes two major assumptions:
- The equation accurately describes the pixel-to-distance relationship across all distances

- If you imagine a plane p that runs normal / perpendicular to the ray that extends directly outward from the camera lens and extends through the reference object, that the pixel-to-distance relationship holds true along all points within the camera’s field of view along that plane
Neither of these assumptions are true in all cases which is the primary reason this technique can only estimate position and lacks accuracy.
A final assumption is that the middle of the camera’s field of view aligns exactly with the heading of the robot.
From Pixels to Position
Assume oroboto’s camera has taken an image of the scene and that we’ve used a yet to be described technique to isolate the reference cube within the image. We’re now in possession of the (x,y) pixel co-ordinates of the cube as well as its width and height in pixels.
described technique to isolate the reference cube within the image. We’re now in possession of the (x,y) pixel co-ordinates of the cube as well as its width and height in pixels.
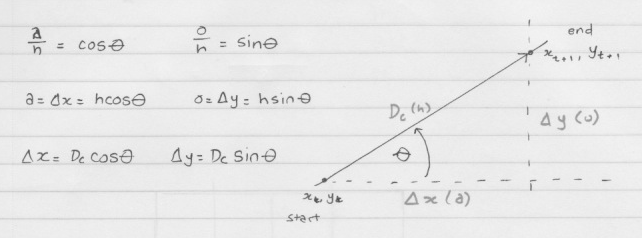
Using the cube’s width in pixels and the pixel-to-distance equation we can estimate (based on assumption #2 above) the physical distance r to the point mid which lies at the intersection of the ray extending directly outward from the camera lens and an imaginary plane p running perpendicular to that ray. Note that mid also lies on the vertical line that equally divides the camera’s image.


Given that we know oroboto’s physical co-ordinates C and heading q at the time the image was captured, we can use simple trigonometry to estimate the physical (x,y) co-ordinates of mid:

Again based on assumption #2, as the reference cube has known physical width (in centimeters) it is possible to calculate the relationship cmPerPx between pixels and centimeters along plane p (ie. how many cm a pixel represents along that plane). The distance in pixels between mid (recall this lies along the vertical line equally dividing the camera’s image) and the reference cube can then be used to estimate od, the physical distance along plane p between mid (whose physical (x,y) co-ordinates were established above) and the reference cube.
Taking the ray r as the new base of a right-angled triangle (which doesn’t look that right-angled in my diagram) more trigonometry yields q’, r’ and from oroboto’s current position C an estimate of the reference cube’s physical co-ordinates:

Isolating the reference cube
The last task is actually locating the red cube within the camera’s image, this is where OpenCV comes in.
In a scene that could contain a multitude of different objects we have two primary “hints” that one of those objects might be ours: its shape and its colour. As we detect and examine objects within the image these will be our primary cues that the object might be the reference cube. Even with these hints we can still be confounded by the fact the shape, which we expect to be a square, could be more trapezoidal or skewed if one of the cube’s faces is off-angle to the camera, and that the colour could appear different depending on lighting conditions. We need to add some robustness to our detection techniques to deal with these cases.
Once the image has been captured it is first converted from RGB (actually BGR, as this is OpenCV’s native representation of RGB) to the HSV (Hue, Saturation, Value) colourspace. Representing the image in HSV is one way to gain some resiliency against varied lighting conditions (shadows, ambient lighting etc).
In HSV, each pixel is specified in terms of its hue (its “core” colour, like “red”), saturation (or “chroma”, this defines the brilliance or intensity of the colour: imagine taking pure red paint and incrementally adding white paint to it such that you move through pinks to pure white) and value (this defines the darkness of a colour or amount of light reflected, imagine taking pure red paint and incrementally adding black paint to it such that you move through rust to pure black). This is useful because it separates colour information from luma (brightness) information. Using HSV, in varied lighting we might expect the saturation and value of the cube’s (red) pixels to vary, but their hue should remain relatively constant. When oroboto is powered on the camera is calibrated to the current environment by placing the red cube in front of it and measuring its average hue. This average, along with a wide range of saturations and values, is used when thresholding incoming images to filter out any pixels that don’t have a similar colour to the cube.
After colourspace conversion, the image is thresholded using OpenCV’s inRange  function. This takes every pixel of the image and compares it to a range of HSV values measured during calibration, turning potentially red (ie. cube) pixels into white and anything else black. The result is a greyscale image with white pixels wherever red pixels had originally been. This is then smoothed using a Gaussian blur to remove noise (the blur eliminates stray white pixels).
function. This takes every pixel of the image and compares it to a range of HSV values measured during calibration, turning potentially red (ie. cube) pixels into white and anything else black. The result is a greyscale image with white pixels wherever red pixels had originally been. This is then smoothed using a Gaussian blur to remove noise (the blur eliminates stray white pixels).
OpenCV offers a range of powerful feature detection algorithms, including findContours, which can extract curves in the image by joining continuous points that have the same colour (which all white pixels in the thresholded image do). We use findContours to extract an external contour (path) around any clusters of white pixels: we hope that one of these clusters resembles a square. For each contour that is found the approxPolyDP function is used to overlay a closed polygon: if that polygon turns out to have 4 sides its aspect ratio is close to 1:1, we’ve found a candidate square. The contours / polygons are iterated to find the best match (the polygon with the aspect ratio closest to 1:1) and if found, this is considered to be the detection of the red cube.
Once isolated the width and height of the cube (in pixels) are known and can be used in the pixel-to-distance equation to start the physical co-ordinate estimation process.
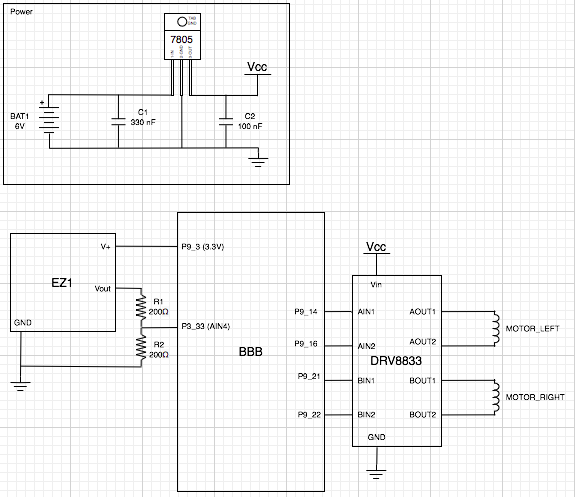
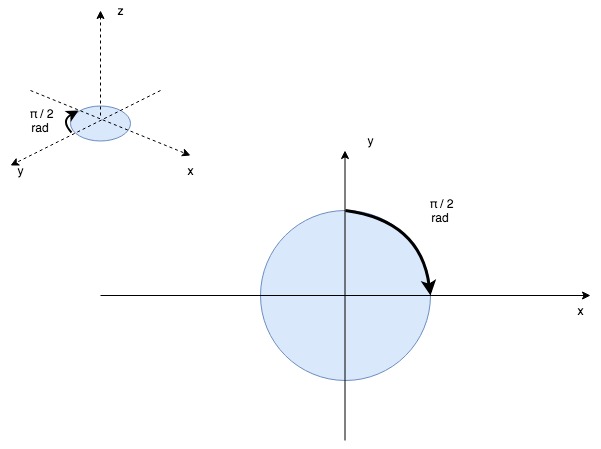
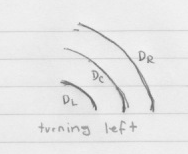
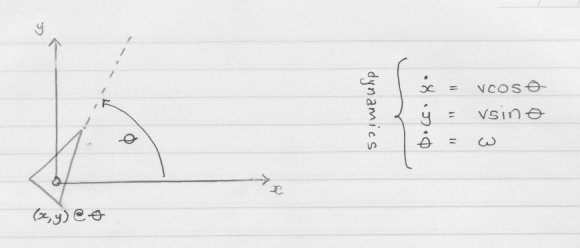
 A differential drive robot’s two wheels are placed horizontally adjacent to each other, as if connected by an axle (their “axis”), and their speed is independently controllable. On most (all?) differential drive robots the axis running through the two wheels also runs through the centre of the bot so that any rotation occurs through its centroid in the x-y plane.
A differential drive robot’s two wheels are placed horizontally adjacent to each other, as if connected by an axle (their “axis”), and their speed is independently controllable. On most (all?) differential drive robots the axis running through the two wheels also runs through the centre of the bot so that any rotation occurs through its centroid in the x-y plane.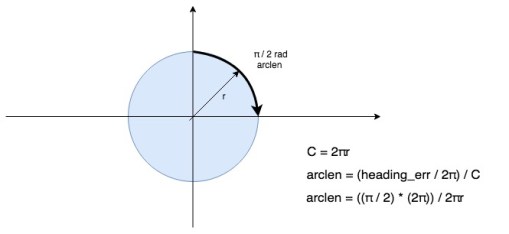


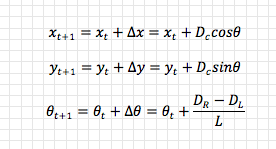

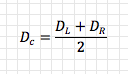
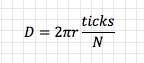

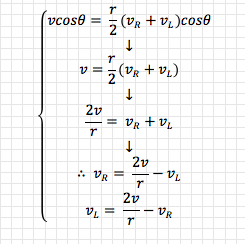
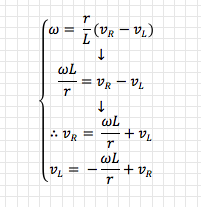
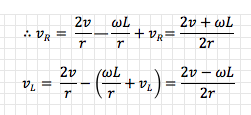



 So far, so good. But how can we put this into practice with the wheel(s) of a robot? A common option is to use a rotary encoder such as the Pololu encoder I have used here. This is an optical encoder and uses two infrared reflectance sensors that shine infrared light onto the inside of the wheel hub, upon which is arranged 12 “teeth” with gaps between them.
So far, so good. But how can we put this into practice with the wheel(s) of a robot? A common option is to use a rotary encoder such as the Pololu encoder I have used here. This is an optical encoder and uses two infrared reflectance sensors that shine infrared light onto the inside of the wheel hub, upon which is arranged 12 “teeth” with gaps between them.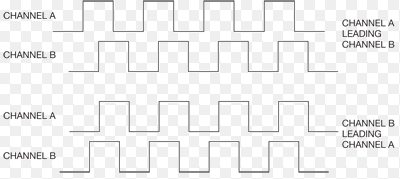
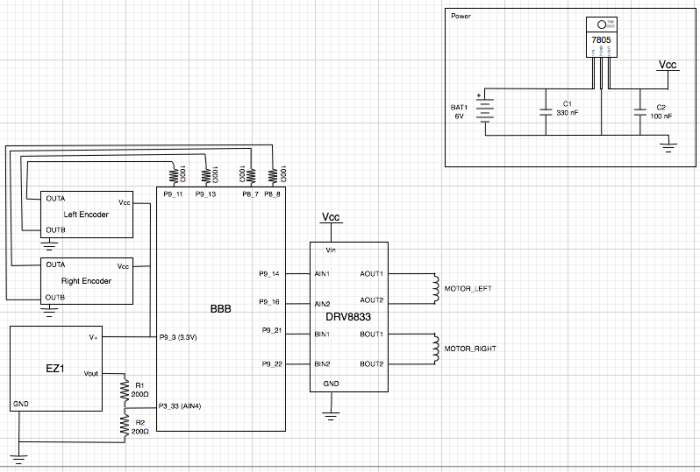
 an amplifier and wave generator for them, along with interfacing them back into timers for distance measurement, but a package like the EZ1 takes care of all of this for you.
an amplifier and wave generator for them, along with interfacing them back into timers for distance measurement, but a package like the EZ1 takes care of all of this for you.